publications | George Miloshevich

2026

PoP
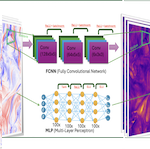Electron Neural Closure for Turbulent Magnetosheath Simulations: Energy Channels

G. Miloshevich, L. Vranckx, F. N. Oliveira Lopes, P. Dazzi, G. Arrò, and 1 more author

Physics of Plasmas, 2026

Abs DOI Bib HTML

In this work, we introduce a non-local five-moment electron pressure tensor closure parametrized by a fully convolutional neural network (FCNN). Electron pressure plays an important role in generalized Ohm’s law, competing with electron inertia. This model is used in the development of a surrogate model for a fully kinetic energy-conserving semi-implicit particle-in-cell simulation of decaying magnetosheath turbulence. We achieve this by training FCNN on a representative set of simulations with a smaller number of particles per cell and showing that our results generalize to a simulation with a large number of particles per cell. We evaluate the statistical properties of the learned equation of state, with a focus on pressure-strain interaction, which is crucial for understanding energy channels in turbulent plasmas. The resulting equation of state learned via FCNN significantly outperforms local closures, such as those learned by multi-layer perceptron (MLP) or double adiabatic expressions. We report that the overall spatial distribution of pressure-strain and its conditional averages are reconstructed well. However, some small-scale features are missed, especially for the off-diagonal components of the pressure tensor. Nevertheless, the results are substantially improved with more training data, indicating favorable scaling and potential for improvement, which will be addressed in future work.
@article{miloshevich2026electron, title = {Electron Neural Closure for Turbulent Magnetosheath Simulations: {{Energy}} Channels}, author = {Miloshevich, G. and Vranckx, L. and de Oliveira Lopes, F. N. and Dazzi, P. and Arrò, G. and Lapenta, G.}, year = {2026}, journal = {Physics of Plasmas}, volume = {33}, number = {1}, pages = {012901}, issn = {1070-664X}, doi = {10.1063/5.0300009}, }

2025

MCSoC
Evaluating Four FPGA-Accelerated Space Use Cases Based on Neural Network Algorithms for On-Board Inference

Pedro Antunes, Muhammad Ihsan Al Hafiz, Jonah Ekelund, Ekaterina Dineva, George Miloshevich, and 2 more authors

In 2025 IEEE 18th International Symposium on Embedded Multicore/Many-core Systems-on-Chip (MCSoC), Dec 2025

Abs DOI Bib HTML

Space missions increasingly deploy high-fidelity sensors that produce data volumes exceeding onboard buffering and downlink capacity. This work evaluates FPGA acceleration of neural networks (NNs) across four space use cases on the AMD ZCU104 board. We use Vitis AI (AMD DPU) and Vitis HLS to implement inference, quantify throughput and energy, and expose toolchain and architectural constraints relevant to deployment. Vitis AI achieves up to 34.16\\times higher inference rate than the embedded ARM CPU baseline, while custom HLS designs reach up to 5.4\\times speedup and add support for operators (e.g., sigmoids, 3D layers) absent in the DPU. For these implementations, measured MPSoC inference power spans 1.56-1.75 W, reducing energy per inference versus CPU execution in all use cases. These results show that NN FPGA acceleration can enable onboard filtering, compression, and event detection, easing downlink pressure in future missions.
@inproceedings{antunesEvaluatingFourFPGAAccelerated2025a, title = {Evaluating {{Four FPGA-Accelerated Space Use Cases Based}} on {{Neural Network Algorithms}} for {{On-Board Inference}}}, author = {Antunes, Pedro and Al Hafiz, Muhammad Ihsan and Ekelund, Jonah and Dineva, Ekaterina and Miloshevich, George and Gonidakis, Panagiotis and Podobas, Artur}, year = {2025}, month = dec, booktitle = {2025 {{IEEE}} 18th {{International Symposium}} on {{Embedded Multicore}}/{{Many-core Systems-on-Chip}} ({{MCSoC}})}, pages = {804--812}, issn = {2771-3075}, doi = {10.1109/MCSoC67473.2025.00126}, url = {https://ieeexplore.ieee.org/abstract/document/11310891}, }
MNRAS
Classifying Solar Flares with kNN on Sparse Autoencoder Representations

Hanne Baeke, G Miloshevich, E Dineva, F Carella, P Gonidakis, and 2 more authors

Monthly Notices of the Royal Astronomical Society, 2025

Abs DOI Bib HTML

The high dimensionality and strong correlations of magnetic field descriptors in the Space-Weather HMI Active Region Patches (SHARPs) dataset present challenges for flare prediction studies. We perform a comparison of dimensionality-reduction pipelines that combine Canonical Factor Analysis (CFA) and sparse autoencoders (SAEs), coupled with a k-Nearest Neighbors classifier, to assess how different feature representations affect predictive skill. We find that both linear (CFA) and nonlinear (SAE) compression enhance flare classification relative to using the raw parameters, with the nonlinear SAE yielding the highest True Skill Statistic (TSS = 0.64) for binary flare/no-flare discrimination. Multiclass predictions remain limited by the imbalance of major flares and by overlapping feature distributions, but performance is consistent across multiple configurations. Our analysis also quantifies the redundancy of SHARP parameters, showing that only 5–7 compressed features are sufficient to capture the predictive information. These results provide a benchmark for dimensionality-reduction strategies in flare forecasting and demonstrate the value of sparse representations for handling correlated astrophysical parameter spaces.
@article{baekeClassifyingSolarFlares2025, title = {Classifying {{Solar Flares}} with {{kNN}} on {{Sparse Autoencoder Representations}}}, author = {Baeke, Hanne and Miloshevich, G and Dineva, E and Carella, F and Gonidakis, P and Amaya, J and Lapenta, G}, year = {2025}, journal = {Monthly Notices of the Royal Astronomical Society}, pages = {staf2271}, issn = {0035-8711}, doi = {10.1093/mnras/staf2271}, }
ApJLett
Prediction of Time-evolving Radial Magnetic Fields on the Solar Surface Using Deep Learning

Hyun-Jin Jeong, Stefaan Poedts, Haopeng Wang, Ekatarina Dineva, Panagiotis Gonidakis, and 4 more authors

The Astrophysical Journal Letters, Aug 2025

Abs DOI Bib HTML

We develop two artificial intelligence–based models (Models A and B) to predict time-evolving photospheric magnetic fields with an adjustable time step, ranging up to one solar rotation later. Model A predicts future magnetic field data using three consecutive radial magnetic field data sets, each 12 hr apart. Model B reconstructs evolving magnetic fields using two sets of three consecutive data sets, one from a given date and the other from 27 days later, each 12 hr apart. To train and evaluate our models, we use a Pix2PixCC-based architecture and radial magnetic field data sets from the Solar Dynamics Observatory/Helioseismic and Magnetic Imager during the solar maximum periods of 2012–2016 and 2021–2023. Models A and B successfully generate magnetic field data corresponding to the input prediction time step. Based on quantitative comparison, Model A outperforms the persistence model and performs comparably to the classical surface flux transport model. Model B shows improved performance compared to both models. We also compare predictions for National Oceanic and Atmospheric Administration Active Regions 12673 and 13664, which rapidly emerged and produced powerful solar flares. Notably, both Models A and B can predict increases in total unsigned magnetic fluxes several days in advance if their evolution is already captured in the input data. Model B also reconstructs radial magnetic fluxes that smoothly overlap between the input data and the model outputs. These results demonstrate the ability of our models to generate time-evolving magnetic field data flexibly and capture emerging magnetic fluxes, which are crucial for heliophysics research and space weather forecasting.
@article{Jeong_2025, doi = {10.3847/2041-8213/adf5c7}, url = {https://doi.org/10.3847/2041-8213/adf5c7}, year = {2025}, month = aug, publisher = {The American Astronomical Society}, volume = {989}, number = {2}, pages = {L31}, author = {Jeong, Hyun-Jin and Poedts, Stefaan and Wang, Haopeng and Dineva, Ekatarina and Gonidakis, Panagiotis and Carella, Francesco and Miloshevich, George and Linan, Luis and Lee, Harim}, title = {Prediction of Time-evolving Radial Magnetic Fields on the Solar Surface Using Deep Learning}, journal = {The Astrophysical Journal Letters}, }

2024

EDS
Extreme heat wave sampling and prediction with analog Markov chain and comparisons with deep learning

George Miloshevich, Dario Lucente, Pascal Yiou, and Freddy Bouchet

Environmental Data Science, 2024

Abs DOI Bib HTML

We present a data-driven emulator, a stochastic weather generator (SWG), suitable for estimating probabilities of prolonged heat waves in France and Scandinavia. This emulator is based on the method of analogs of circulation to which we add temperature and soil moisture as predictor fields. We train the emulator on an intermediate complexity climate model run and show that it is capable of predicting conditional probabilities (forecasting) of heat waves out of sample. Special attention is payed that this prediction is evaluated using a proper score appropriate for rare events. To accelerate the computation of analogs, dimensionality reduction techniques are applied and the performance is evaluated. The probabilistic prediction achieved with SWG is compared with the one achieved with a convolutional neural network (CNN). With the availability of hundreds of years of training data, CNNs perform better at the task of probabilistic prediction. In addition, we show that the SWG emulator trained on 80 years of data is capable of estimating extreme return times of order of thousands of years for heat waves longer than several days more precisely than the fit based on generalized extreme value distribution. Finally, the quality of its synthetic extreme teleconnection patterns obtained with SWG is studied. We showcase two examples of such synthetic teleconnection patterns for heat waves in France and Scandinavia that compare favorably to the very long climate model control run.
@article{miloshevich2023extreme, title = {Extreme heat wave sampling and prediction with analog Markov chain and comparisons with deep learning}, volume = {3}, doi = {10.1017/eds.2024.7}, journal = {Environmental Data Science}, author = {Miloshevich, George and Lucente, Dario and Yiou, Pascal and Bouchet, Freddy}, year = {2024}, pages = {e9}, url = {https://doi.org/10.1017/eds.2024.7}, }

2023

Fr. Earth Sc.
Robust intra-model teleconnection patterns for extreme heatwaves

George Miloshevich, Philippine Rouby-Poizat, Francesco Ragone, and Freddy Bouchet

Frontiers in Earth Science, 2023

Abs DOI Bib HTML

Introduction: The goal of this study is to provide analysis of statistics and dynamics of extreme heatwaves over two areas of Europe, France and Scandinavia, while comparing and contrasting the representation in climate models and reanalysis.Methods: The 1000 year long datasets are generated using respectively two climate models of different complexity. The composite maps of the heatwaves found in these datasets are compared to the ones observed in reanalysis by estimating significance of such patterns. We also employ time series analysis, in particular compare return time plots and use Gaussian stochastic processes to model the temporal correlations for rare events.Results: Our investigation reveals that recurrent wavenumber three teleconnection patterns distinctly underpin heatwaves in France and Scandinavia. These patterns manifest in both surface temperature and mid-tropospheric geopotential height. For heatwaves of return times of 4 years such patterns are robustly represented across diverse models of complexity and reanalysis data. For longer return times, reanalysis records are too short to give statistically significant results, while models confirm the relevance of these large scale patterns for the most extreme heatwaves. Moreover, A time series analysis shows that heatwave indices defined at synoptic scale are fairly well described by Gaussian stochastic processes, and that these Gaussian processes reproduce well return time plots even for very rare events.Discussion: These results suggest that extreme heatwaves over different areas of Europe show recurrent typical behaviours in terms of long-range spatial correlations and subseasonal-scale temporal correlations. These properties are consistently represented among models of different complexity and observations, thus suggesting their relevance for a better understanding of the drivers and causes of the occurrence of extreme midlatitude heatwaves and their predictability.
@article{miloshevich2023robust, author = {Miloshevich, George and Rouby-Poizat, Philippine and Ragone, Francesco and Bouchet, Freddy}, title = {Robust intra-model teleconnection patterns for extreme heatwaves}, journal = {Frontiers in Earth Science}, volume = {11}, year = {2023}, url = {https://www.frontiersin.org/articles/10.3389/feart.2023.1235579}, doi = {10.3389/feart.2023.1235579}, issn = {2296-6463} }
NaturePrt.J.
Ensembles of climate simulations to anticipate worst case heatwaves during the Paris 2024 Olympics

Pascal Yiou, Camille Cadiou, Davide Faranda, Aglaé Jézéquel, Nemo Malhomme, and 5 more authors

npj Climate and Atmospheric Science, Nov 2023

Abs DOI Bib HTML

The Summer Olympic Games in 2024 will take place during the apex of the temperature seasonal cycle in the Paris Area. The mid-latitudes of the Northern hemisphere have witnessed a few intense heatwaves since the 2003 event. Those heatwaves have had environmental and health impacts, which often came as surprises. In this paper, we search for the most extreme heatwaves in Ile-de-France that are physically plausible, under climate change scenarios, for the decades around 2024. We circumvent the sampling limitation by applying a rare event algorithm on CMIP6 data to evaluate the range of such extremes. We find that the 2003 record can be exceeded by more than 4 \,^∘C in Ile-de-France before 2050, with a combination of prevailing anticyclonic conditions and cut-off lows. This study intends to raise awareness of those unprecedented events, against which our societies are ill-prepared, in spite of adaptation measures designed from previous events. Those results could be extended to other areas of the world.
@article{yiou:hal-03921111, author = {Yiou, Pascal and Cadiou, Camille and Faranda, Davide and J{\'e}z{\'e}quel, Agla{\'e} and Malhomme, Nemo and Miloshevich, George and Noyelle, Robin and Pons, Flavio and Robin, Yoann and Vrac, Mathieu}, doi = {10.1038/s41612-023-00500-5}, id = {Yiou2023}, isbn = {2397-3722}, journal = {npj Climate and Atmospheric Science}, number = {1}, pages = {188}, title = {Ensembles of climate simulations to anticipate worst case heatwaves during the Paris 2024 Olympics}, url = {https://doi.org/10.1038/s41612-023-00500-5}, volume = {6}, month = nov, year = {2023}, bdsk-url-1 = {https://doi.org/10.1038/s41612-023-00500-5} }
PRFluids
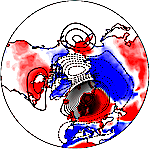Probabilistic forecasts of extreme heatwaves using convolutional neural networks in a regime of lack of data

George Miloshevich, Bastien Cozian, Patrice Abry, Pierre Borgnat, and Freddy Bouchet

Phys. Rev. Fluids, Apr 2023

Abs DOI Bib HTML PDF Slides

Understanding extreme events and their probability is key for the study of climate change impacts, risk assessment, adaptation, and the protection of living beings. Extreme heatwaves are, and likely will be in the future, among the deadliest weather events. Forecasting their occurrence probability a few days, weeks, or months in advance is a primary challenge for risk assessment and attribution but also for fundamental studies about processes, dataset and model validation, and climate change studies. In this work we develop a methodology to build forecasting models which are based on convolutional neural networks, trained on extremely long 8000-year climate model outputs. This approach is parallel to weather model forecasting and has complementary scopes. Because the relation between extreme events is intrinsically probabilistic, we emphasize probabilistic forecast and validation. We demonstrate that neural networks have positive predictive skills, with respect to random climatological forecasts, for the occurrence of long-lasting 14-day heatwaves over France, up to 15 days ahead of time for fast dynamical drivers (500 hPa geopotential height fields), and also at much longer lead times for slow physical drivers (soil moisture). This forecast is made seamlessly in time and space, for fast hemispheric and slow local drivers. The method is easily implemented and versatile. We find that the neural network selects extreme heatwaves associated with a north hemisphere wave-number 3 pattern. We argue that this machine learning approach should be key in the future for quantitative process studies, model intercomparisons, and dataset studies. For instance, we find that the 2 meter temperature field does not contain any new useful statistical information for heatwave forecast, when added to the 500 hPa geopotential height and soil moisture fields. The main scientific message is that most of the times, training neural networks for predicting extreme heatwaves occurs in a regime of lack of data. We suggest that this is likely to be the case for most other applications to large-scale atmosphere and climate phenomena. Depending on the information to be learned, training might require dataset lengths as long as several thousands of years, or even more, for optimal forecasting skill. For instance, using 100-year-long training sets, a regime of drastic lack of data, leads to severely lower predictive skills and general inability to extract useful information available in the 500 hPa geopotential height field at a hemispheric scale in contrast to the dataset of several thousand years long. Even with several-thousand-year-long datasets, no convergence is observed in the predictive skills coming from hemispheric geopotential height fields. We discuss perspectives for dealing with the lack of data regime, for instance, rare event simulations and how transfer learning may play a role in this latter task.
@article{miloshevich2022probabilistic, title = {Probabilistic forecasts of extreme heatwaves using convolutional neural networks in a regime of lack of data}, author = {Miloshevich, George and Cozian, Bastien and Abry, Patrice and Borgnat, Pierre and Bouchet, Freddy}, journal = {Phys. Rev. Fluids}, volume = {8}, issue = {4}, pages = {040501}, numpages = {40}, year = {2023}, month = apr, publisher = {American Physical Society}, doi = {10.1103/PhysRevFluids.8.040501}, url = {https://link.aps.org/doi/10.1103/PhysRevFluids.8.040501}, media = {https://www.youtube.com/watch?v=-gJgLoPb15U}, hal_id = {hal-03741938}, hal_version = {v2}, }

2022

2021

JPP
Inverse cascade and magnetic vortices in kinetic Alfvén-wave turbulence

G. Miloshevich, D. Laveder, T. Passot, and P. L. Sulem

Journal of Plasma Physics, 2021

Abs DOI Bib HTML PDF

The main goal of this article is to explore the possible sources for large-scale coherent magnetic structures that can be created in turbulent electron-proton plasmas. We work with the model developed for applications to solar wind, which is obtained as a fluid closure of gyrokinetic equations that describe magnetized collisionless plasmas. It can be thought of as a generalisation of magnetohydrodynamics spaning the scales above and below the ion Larmor radius (intermediate scale), which leads to nonlinear dispersive phenomenology of interacting kinetic Alfvén waves (KAW). The chief quantity of interest is Generalized Cross Helicity (GCH) which measures the energy of imbalance between the two KAW eigenmodes. At large scales they merge with Alfvén wave branches which propagate forward and backward relative to the magnetic field line. It was known that at large scales the cascade is forward like in usual Kolmogorov phenomenology and there were theoretical reasons to believe the cascade reversed sign at small scales. Using 3D numerical simulations we have found that the inverse cascade is suppressed at intermediate scales, which leads to the formation of large elongated magnetic vortices on the Larmor scale (termed finite-scale condensate). This is interesting since it is perhaps related to the result by another group (Meyrand at al 2021), whereby the forward cascade in the similar system was also suppressed at the Larmor scale. This process can potentially explain ion-kinetic spectral breaks in plasma turbulence, and provide theory alternative to that of, where the effects of Landau damping were phenomenologically included. Furthermore, we study the decay instability of KAW, i.e. the decay of a pump mode into two daughter modes, one with larger wavenumber and one with smaller. This is resonant behavior which is possible due to the dispersive nature of KAW. Related to these events are instabilities of the balanced state (between the two KAW eigenmodes)
@article{miloshevich_laveder_passot_sulem_2021, title = {Inverse cascade and magnetic vortices in kinetic Alfvén-wave turbulence}, volume = {87}, doi = {10.1017/S0022377820001531}, number = {2}, journal = {Journal of Plasma Physics}, publisher = {Cambridge University Press}, author = {Miloshevich, G. and Laveder, D. and Passot, T. and Sulem, P. L.}, year = {2021}, pages = {905870201}, media = {https://wavecomplexity.univ-cotedazur.fr/seminars/george_miloshevich/}, }
JPP
Hamiltonian reduction of Vlasov–Maxwell to a dark slow manifold

George Miloshevich and Joshua W. Burby

Journal of Plasma Physics, 2021

Abs DOI Bib HTML PDF

One of the challenges involved in modeling processes in collsionless plasmas is related to their multi-scale and multi-species nature. This motivates reductions, i.e. approximations, which are sometimes performed in an uncontrolled way, without maintaining conservation laws. We stipulate that the conservation laws such as energy and momentum and the associated symmetries actually play a crucial role in physics. In this paper we perform a formal asymptotic expansion and introduce the slow manifold on which the dynamics is constrained so that electromagnetic waves are eliminated. In particular, having in mind elimination of fast modes (electromagnetic waves), expansion of Maxwell-Vlasov system is performed and a sequence of reduced models are derived which include: Vlasov-Poisson and Vlasov-Darwin but also the next order expansion, which couples the transverse electromagnetic field to the Braginskii pressure tensor and the magnetic field to the charge-weighted heat flux tensor. The latter effect has not been considered earlier to our knowledge. One of the possible applications for this family of models is to avoid spurious radiation noise in Particle-in-Cell codes, which are commonly used in plasma simulations. This would thus require discretization techniques, which can be performed directly within the Hamiltonian action principle formalism. In the remainder of the paper (which is more interesting for mathematical physicists) the heuristic time scale is derived on which the state prepared on the dark slow manifold remains asymptotically close to it. In the dimensionless units the expansion depends on the small parameter that is inversely proportional to speed of light. When the former is set to zero Vlasov-Poisson model is recovered. Straightforward truncation of the Poisson bracket may not conserve the Jacobi identity, which is a crucial ingredient for the Hamiltonian theory. Without it Darboux’s theorem is violated and local canonical variables may not exist. Most fundamental physical models we are aware of satisfy Jacobi identity. Thus alternative approach is undertaken, whereby instead of truncating Poisson bracket, which has no geometric interpretation, we truncate the conjugate two-form Ω. This approach can be thought of as an infinite dimensional generalization of a Lie-transform. It is infinite dimensional because our phase space is spanned by a group of transformations of the distribution function f (similar to Euler-Lagrange maps) as well as 3-dimensional electric E and magnetic fields B. In a nutshell, using language of differential forms we find a coordinate-free transformation of variables that “rectifies” symplectic two-form Ω of the dark slow manifold onto the one of the Vlasov-Poisson system. As a consequence, Hamiltonian and the Poisson bracket are recovered in the new coordinates, so that the new Poisson bracket is actually equivalent to the more simple one given by Vlasov-Poisson. The resulting equations of motion are also derived. The procedure ensures that the approximations we made preserve the sought for Hamiltonian structure.
@article{miloshevich_burby_2021, title = {Hamiltonian reduction of Vlasov–Maxwell to a dark slow manifold}, volume = {87}, doi = {10.1017/S0022377821000556}, number = {3}, journal = {Journal of Plasma Physics}, publisher = {Cambridge University Press}, author = {Miloshevich, George and Burby, Joshua W.}, year = {2021}, pages = {835870301}, }

2019

ApJLett
Modeling Imbalanced Collisionless Alfvén Wave Turbulence with Nonlinear Diffusion Equations

G. Miloshevich, T. Passot, and P. L. Sulem

The Astrophysical Journal Letters, Dec 2019

Abs DOI Bib HTML PDF Slides

A pair of nonlinear diffusion equations in Fourier space is used to study the dynamics of strong Alfvén wave turbulence, from MHD to electron scales. Special attention is paid to the regime of imbalance between the energies of counter-propagating waves commonly observed in the solar wind (SW), especially in regions relatively close to the Sun. In the collisionless regime where dispersive effects arise at scales comparable to or larger than those where dissipation becomes effective, the imbalance produced by a given injection rate of generalized cross-helicity (GCH), which is an invariant, is much larger than in the corresponding collisional regime described by the usual (or reduced) magnetohydrodynamics. The combined effect of high imbalance and ion Landau damping induces a steep energy spectrum for the transverse magnetic field at sub-ion scales. This spectrum is consistent with observations in highly Alfvénic regions of the SW, such as trailing edges, but does not take the form of a transition range continued at smaller scales by a shallower spectrum. This suggests that the observed spectra displaying such a transition result from the superposition of contributions originating from various streams with different degrees of imbalance. Furthermore, when imbalanced energy injection is supplemented at small scales in an already fully developed turbulence, for example under the effect of magnetic reconnection, a significant enhancement of the imbalance at all scales is observed.
@article{Miloshevich_2019, doi = {10.3847/2041-8213/ab60b1}, url = {https://iopscience.iop.org/article/10.3847/2041-8213/ab60b1/meta}, year = {2019}, month = dec, publisher = {American Astronomical Society}, volume = {888}, number = {1}, pages = {L7}, author = {Miloshevich, G. and Passot, T. and Sulem, P. L.}, title = {Modeling Imbalanced Collisionless Alfv{\'{e}}n Wave Turbulence with Nonlinear Diffusion Equations}, journal = {The Astrophysical Journal Letters}, }

2018

PoP
Direction of cascades in a magnetofluid model with electron skin depth and ion sound Larmor radius scales

George Miloshevich, Philip J. Morrison, and Emanuele Tassi

Physics of Plasmas, 2018

Abs DOI Bib HTML PDF Slides

The direction of cascades in a two-dimensional model that takes electron inertia and ion sound Larmor radius into account is studied, resulting in analytical expressions for the absolute equilibrium states of the energy and helicities. These states suggest that typically both the energy and magnetic helicity at scales shorter than the electron skin depth have a direct cascade, while at large scales the helicity has an inverse cascade as established earlier for reduced magnetohydrodynamics (MHD). The calculations imply that the introduction of gyro-effects allows for the existence of negative temperature (conjugate to energy) states and the condensation of energy to the large scales. Comparisons between two- and three-dimensional extended MHD models (MHD with two-fluid effects) show qualitative agreement between the two.
@article{doi:10.1063/1.5023089, author = {Miloshevich, George and Morrison, Philip J. and Tassi, Emanuele}, title = {Direction of cascades in a magnetofluid model with electron skin depth and ion sound Larmor radius scales}, journal = {Physics of Plasmas}, volume = {25}, number = {7}, pages = {072303}, year = {2018}, doi = {10.1063/1.5023089}, url = {https://doi.org/10.1063/1.5023089}, }

2017

JPAM
Traveling solitons in long-range oscillator chains

George Miloshevich, Jean Pierre Nguenang, Thierry Dauxois, Ramaz Khomeriki, and Stefano Ruffo

Journal of Physics A: Mathematical and Theoretical, Feb 2017

Abs DOI Bib HTML PDF

We investigate the existence and propagation of solitons in a long-range extension of the quartic Fermi–Pasta–Ulam (FPU) chain of anharmonic oscillators. The coupling in the linear term decays as a power-law with an exponent 1<α\leqslant 3 . We obtain an analytic perturbative expression of traveling envelope solitons by introducing a non linear Schrödinger equation for the slowly varying amplitude of short wavelength modes. Due to the non analytic properties of the dispersion relation, it is crucial to develop the theory using discrete difference operators. Those properties are also the ultimate reason why kink-solitons may exist but are unstable, at variance with the short-range FPU model. We successfully compare these approximate analytic results with numerical simulations for the value α=2 which was chosen as a case study.
@article{Miloshevich_2017, doi = {10.1088/1751-8121/aa5fcf}, url = {https://doi.org/10.1088/1751-8121/aa5fcf}, year = {2017}, month = feb, publisher = {{IOP} Publishing}, volume = {50}, number = {12}, pages = {12LT02}, author = {Miloshevich, George and Nguenang, Jean Pierre and Dauxois, Thierry and Khomeriki, Ramaz and Ruffo, Stefano}, title = {Traveling solitons in long-range oscillator chains}, journal = {Journal of Physics A: Mathematical and Theoretical}, }
PoP
Action principles for relativistic extended magnetohydrodynamics: A unified theory of magnetofluid models

Yohei Kawazura, George Miloshevich, and Philip J. Morrison

Physics of Plasmas, 2017

Abs DOI Bib HTML PDF Poster

Two types of Eulerian action principles for relativistic extended magnetohydrodynamics (MHD) are formulated. With the first, the action is extremized under the constraints of density, entropy, and Lagrangian label conservation, which leads to a Clebsch representation for a generalized momentum and a generalized vector potential. The second action arises upon transformation to physical field variables, giving rise to a covariant bracket action principle, i.e., a variational principle in which constrained variations are generated by a degenerate Poisson bracket. Upon taking appropriate limits, the action principles lead to relativistic Hall MHD and well-known relativistic ideal MHD. For the first time, the Hamiltonian formulation of relativistic Hall MHD with electron thermal inertia (akin to Comisso et al., Phys. Rev. Lett. 113, 045001 (2014) for the electron–positron plasma) is introduced. This thermal inertia effect allows for violation of the frozen-in magnetic flux condition in marked contrast to nonrelativistic Hall MHD that does satisfy the frozen-in condition. We also find the violation of the frozen-in condition is accompanied by freezing-in of an alternative flux determined by a generalized vector potential. Finally, we derive a more general 3 + 1 Poisson bracket for nonrelativistic extended MHD, one that does not assume smallness of the electron ion mass ratio.
@article{doi:10.1063/1.4975013, author = {Kawazura, Yohei and Miloshevich, George and Morrison, Philip J.}, title = {Action principles for relativistic extended magnetohydrodynamics: A unified theory of magnetofluid models}, journal = {Physics of Plasmas}, volume = {24}, number = {2}, pages = {022103}, year = {2017}, doi = {10.1063/1.4975013}, url = {https://doi.org/10.1063/1.4975013}, }
NJP
On the structure and statistical theory of turbulence of extended magnetohydrodynamics

George Miloshevich, Manasvi Lingam, and Philip J Morrison

New Journal of Physics, Jan 2017

Abs DOI Bib HTML PDF

Recent progress regarding the noncanonical Hamiltonian formulation of extended magnetohydrodynamics (XMHD), a model with Hall drift and electron inertia, is summarized. The advantages of the Hamiltonian approach are invoked to study some general properties of XMHD turbulence, and to compare them against their ideal MHD counterparts. For instance, the helicity flux transfer rates for XMHD are computed, and Liouville’s theorem for this model is also verified. The latter is used, in conjunction with the absolute equilibrium states, to arrive at the spectra for the invariants, and to determine the direction of the cascades, e.g., generalizations of the well-known ideal MHD inverse cascade of magnetic helicity. After a similar analysis is conducted for XMHD by inspecting second order structure functions and absolute equilibrium states, a couple of interesting results emerge. When cross helicity is taken to be ignorable, the inverse cascade of injected magnetic helicity also occurs in the Hall MHD range—this is shown to be consistent with previous results in the literature. In contrast, in the inertial MHD range, viz at scales smaller than the electron skin depth, all spectral quantities are expected to undergo direct cascading. The consequences and relevance of our results in space and astrophysical plasmas are also briefly discussed.
@article{Miloshevich_2018, doi = {10.1088/1367-2630/aa55eb}, url = {https://doi.org/10.1088/1367-2630/aa55eb}, year = {2017}, month = jan, publisher = {{IOP} Publishing}, volume = {19}, number = {1}, pages = {015007}, author = {Miloshevich, George and Lingam, Manasvi and Morrison, Philip J}, title = {On the structure and statistical theory of turbulence of extended magnetohydrodynamics}, journal = {New Journal of Physics}, }

2016

PLA
Concomitant Hamiltonian and topological structures of extended magnetohydrodynamics

Manasvi Lingam, George Miloshevich, and Philip J. Morrison

Physics Letters A, 2016

Abs DOI Bib HTML PDF Poster

The paper describes the unique geometric properties of ideal magnetohydrodynamics (MHD), and demonstrates how such features are inherited by extended MHD, viz. models that incorporate two-fluid effects (the Hall term and electron inertia). The generalized helicities, and other geometric expressions for these models are presented in a topological context, emphasizing their universal facets. Some of the results presented include: the generalized Kelvin circulation theorems; the existence of two Lie-dragged 2-forms; and two concomitant helicities that can be studied via the Jones polynomial, which is widely utilized in Chern–Simons theory. The ensuing commonality is traced to the existence of an underlying Hamiltonian structure for all the extended MHD models, exemplified by the presence of a unique noncanonical Poisson bracket, and its associated energy.
@article{LINGAM20162400, title = {Concomitant Hamiltonian and topological structures of extended magnetohydrodynamics}, journal = {Physics Letters A}, volume = {380}, number = {31}, pages = {2400-2406}, year = {2016}, issn = {0375-9601}, doi = {https://doi.org/10.1016/j.physleta.2016.05.024}, url = {https://www.sciencedirect.com/science/article/pii/S037596011630216X}, author = {Lingam, Manasvi and Miloshevich, George and Morrison, Philip J.}, }

2015

PoP
Remarkable connections between extended magnetohydrodynamics models

M. Lingam, P. J. Morrison, and G. Miloshevich

Physics of Plasmas, 2015

Abs DOI Bib HTML PDF

Through the use of suitable variable transformations, the commonality of all extended magnetohydrodynamics (MHD) models is established. Remarkable correspondences between the Poisson brackets of inertialess Hall MHD and inertial MHD (which has electron inertia, but not the Hall drift) and extended MHD (which has both effects) are established. The helicities (two in all) for each of these models are obtained through these correspondences. The commonality of all the extended MHD models is traced to the existence of two Lie-dragged 2-forms, which are closely associated with the canonical momenta of the two underlying species. The Lie-dragging of these 2-forms by suitable velocities also leads to the correct equations of motion. The Hall MHD Poisson bracket is analyzed in detail, the Jacobi identity is verified through a detailed proof, and this proof ensures the Jacobi identity for the Poisson brackets of all the models.
@article{doi:10.1063/1.4926821, author = {Lingam, M. and Morrison, P. J. and Miloshevich, G.}, title = {Remarkable connections between extended magnetohydrodynamics models}, journal = {Physics of Plasmas}, volume = {22}, number = {7}, pages = {072111}, year = {2015}, doi = {10.1063/1.4926821}, url = {https://doi.org/10.1063/1.4926821}, }
PRE
Instabilities and relaxation to equilibrium in long-range oscillator chains

George Miloshevich, Jean-Pierre Nguenang, Thierry Dauxois, Ramaz Khomeriki, and Stefano Ruffo

Phys. Rev. E, Mar 2015

Abs DOI Bib HTML PDF

We study instabilities and relaxation to equilibrium in a long-range extension of the Fermi-Pasta-Ulam-Tsingou (FPU) oscillator chain by exciting initially the lowest Fourier mode. Localization in mode space is stronger for the long-range FPU model. This allows us to uncover the sporadic nature of instabilities, i.e., by varying initially the excitation amplitude of the lowest mode, which is the control parameter, instabilities occur in narrow amplitude intervals. Only for sufficiently large values of the amplitude, the system enters a permanently unstable regime. These findings also clarify the long-standing problem of the relaxation to equilibrium in the short-range FPU model. Because of the weaker localization in mode space of this latter model, the transfer of energy is retarded and relaxation occurs on a much longer timescale.
@article{PhysRevE.91.032927, title = {Instabilities and relaxation to equilibrium in long-range oscillator chains}, author = {Miloshevich, George and Nguenang, Jean-Pierre and Dauxois, Thierry and Khomeriki, Ramaz and Ruffo, Stefano}, journal = {Phys. Rev. E}, volume = {91}, issue = {3}, pages = {032927}, numpages = {5}, year = {2015}, month = mar, publisher = {American Physical Society}, doi = {10.1103/PhysRevE.91.032927}, url = {https://link.aps.org/doi/10.1103/PhysRevE.91.032927}, }

2013

EPL
Dipolar needles in the microcanonical ensemble: Evidence of spontaneous magnetization and ergodicity breaking

George Miloshevich, Thierry Dauxois, Ramaz Khomeriki, and Stefano Ruffo

EPL (Europhysics Letters), Oct 2013

Abs DOI Bib HTML PDF

A family of Ising models with long-range interactions was known to have gaps in magnetization to which no microscopic configuration corresponds. Long range systems have many other interesting statistical physics phenomena, such as ensemble inequivalence (canonical and microcanonical) and negative specific heat to name a few. In this letter we studied a needle-like (long) lattices of dipolar spins and we have shown that their Hamiltonian can be mapped to aforementioned long-range Ising model using some heuristic arguments. As such it motivates this family of Ising models and can be considered a more physical realization thereof. Such systems can be motivated by the experiments with some rare-earth compounds and nanoparticle essemblies. The mapping allows us to identify phase transitions in our samples of dipolar needles with the ones of the Ising model. These phase transitions involve ferromagnetic, paramagnetic and meta-stable states which lead to telegraph noise-type transitions between such states in the metastable region, that we observe with direct numerical simulations. The precise onset of the phase transitions can be determined from the control parameters such as the length of our samples as well as the type of lattice we use (simple cubic, face centered, body centered). The results from numerical simulations are duly compared to analytical estimates with relatively good agreement. The overall mechanism of the transitions between different states can be motivated by anti-ferromagnetic nearest-neighbor and ferromagnetic mean-field coupling. We believe that the result crucially depends on the long-range nature of the spin interaction in our system. For this we have estimated the correlation length one would expect from a short range system, which turns out to be roughly the size of the lattice constant, thus clearly too small. This fact suggests that the magnetization order we observe is not of a short-range character
@article{Miloshevich_2013, doi = {10.1209/0295-5075/104/17011}, url = {https://doi.org/10.1209/0295-5075/104/17011}, year = {2013}, month = oct, publisher = {{IOP} Publishing}, volume = {104}, number = {1}, pages = {17011}, author = {Miloshevich, George and Dauxois, Thierry and Khomeriki, Ramaz and Ruffo, Stefano}, title = {Dipolar needles in the microcanonical ensemble: Evidence of spontaneous magnetization and ergodicity breaking}, journal = {{EPL} (Europhysics Letters)}, }

2009

PRL
Stochastic Resonance in the Fermi-Pasta-Ulam Chain

George Miloshevich, Ramaz Khomeriki, and Stefano Ruffo

Phys. Rev. Lett., Jan 2009

Abs DOI Bib HTML PDF

We consider a damped β-Fermi-Pasta-Ulam chain, driven at one boundary subjected to stochastic noise. It is shown that, for a fixed driving amplitude and frequency, increasing the noise intensity, the system’s energy resonantly responds to the modulating frequency of the forcing signal. Multiple peaks appear in the signal-to-noise ratio, signaling the phenomenon of stochastic resonance. The presence of multiple peaks is explained by the existence of many stable and metastable states that are found when solving this boundary value problem for a semicontinuum approximation of the model. Stochastic resonance is shown to be generated by transitions between these states.
@article{PhysRevLett.102.020602, url = {https://link.aps.org/doi/10.1103/PhysRevLett.102.020602}, title = {Stochastic Resonance in the Fermi-Pasta-Ulam Chain}, author = {Miloshevich, George and Khomeriki, Ramaz and Ruffo, Stefano}, journal = {Phys. Rev. Lett.}, volume = {102}, issue = {2}, pages = {020602}, numpages = {4}, year = {2009}, month = jan, publisher = {American Physical Society}, doi = {10.1103/PhysRevLett.102.020602}, }