Turbulence in Plasmas
Inverse cascade in gyrofluids
In this project the idea is to model ion and sub-ion scales that one finds in solar wind turbulence of forward and backward propagating Alfvèn waves (AW). Solar wind is ejected from the sun and propagets through heliosphere before reaching the Earth’s magnetosphere. Of particular interest for us was Kinetic Alfvèn Wave (KAW) turbulence which is a oblique dispersive wave that continues the AW spectrum to the small scales. There are various questions in solar wind community related to spectral breaks at ion scales and heating of solar wind all the way down to electron scales. These scales are related to motion of charged particles in self-consistent fields.
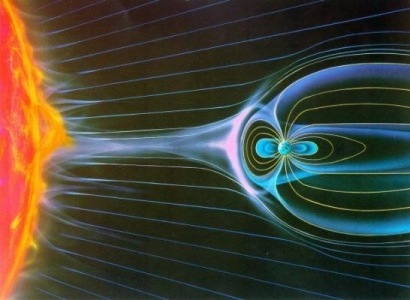
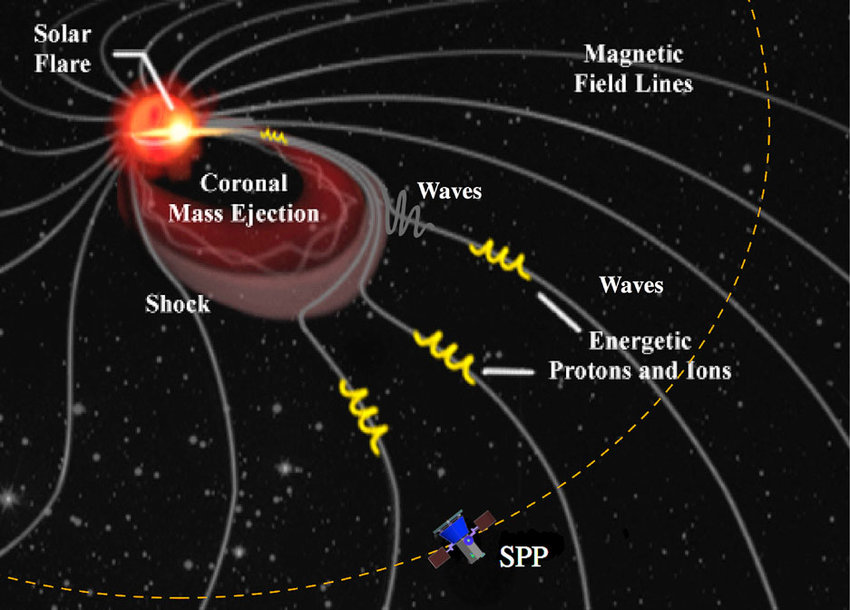
We use a model (gyrofluid) that assumes isothermal electrons and is obtained from kinetics under a set of approximations. The motivation behind using gyrofluids is that they are much cheaper to run than gyrokinetic or full kinetic code. The two important quantities of interest are total energy and Generalized Cross Helicity GCH
and
\[E_{GCH} \sim \int d^3\,x\, ( E_+ - E_- )/V_{ph},\]where \(V_{ph}\) is the KAW phase velocity. The system of equations is modelled numerically using pseuspectral code. We inject forward \(E_+\) and backward \(E_-\) propagating waves at a range of small wavenumbers and observe the inverse transfer of GCH.

We varied the parameters of the driving mode to study the impact they have on such vortices. Control parameters where the forcing wavenumber \(k_f\) and electron beta \(beta_e\) which is defined as the ratio of the pressure and magnetic field. We found that the inverse transfer is limited above \(\beta_e\sim 4\) which interestingly corresponds to the depression in the dispersion relation of KAW.
The second component of our work was to study decay instability which consists of a pump mode generating two daughter modes. This is possible if the resonance manifold exists, which is guaranteed by the KAW dispersive nature. So once enough energy is injected this weak turbulence regime is no longer detectible in simulations.
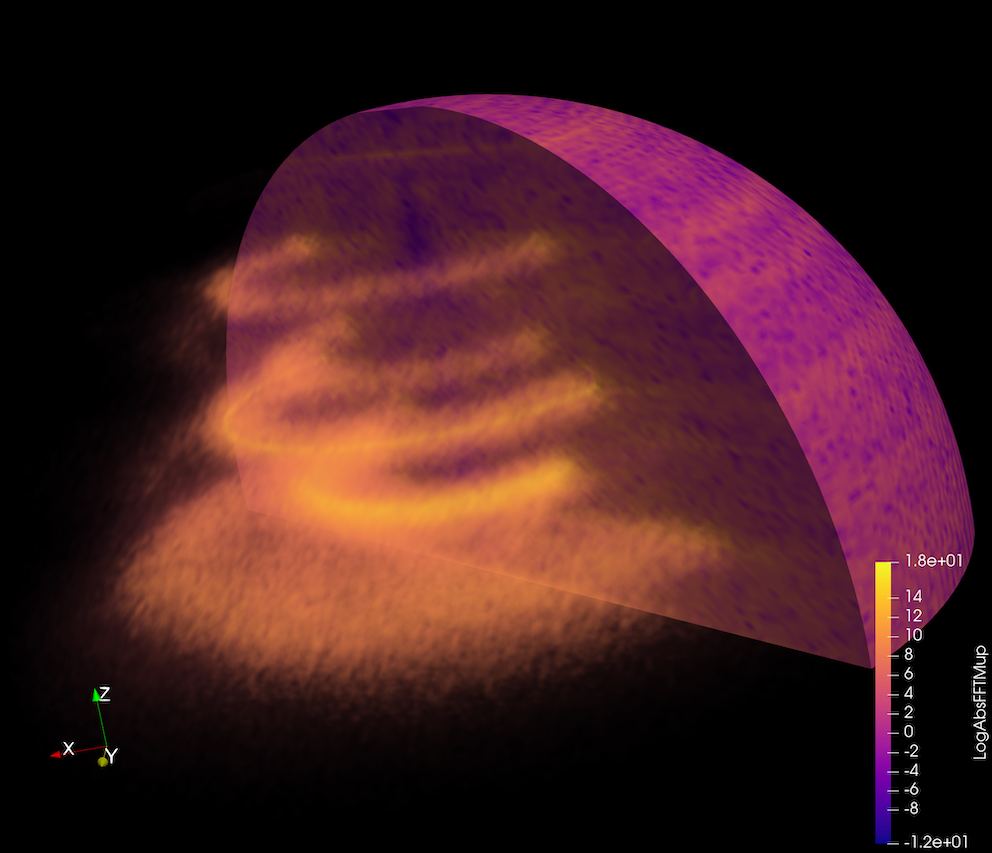
Our work culminates with showing small nonlinear parameter which controls the regime. If the turbulence gets too strong the simple 3-wave resonance picture is washed out
\[\chi_f\sim\frac{(k_f v_{ph})^{-1}}{\tau_{NL}} \sim\epsilon_E^{1/3}k_\perp^{1/3}\beta_e^{1/2}k_\|^{-1},\]where \(k_f\) is the forcing wavenumber, \(\beta_e\) electron beta, or the ratio of pressure and magnetic energy.